|
From quick sync to quick ship (Sponsored)
Most AI notetakers just transcribe.
Granola is the AI notepad that helps you stay focused in meetings, then turns your conversations into real progress.
Engineers use Granola to:
Draft Linear/Jira tickets from standup notes
Paste code into Granola Chat and instantly receive a pass/fail verdict against the requirements that were discussed in your meeting.
Search across weeks of conversations in project folders
Create custom prompts for recurring meetings (TL;DR, decision log, action items) with Recipes
Granola works with your device audio, so no bots join your meetings. Use with any meeting app, like Zoom, Meet or Teams, and in-person with Granola for iPhone.
1 months off any paid plan with the code BYTEBYTEGO
When we write a few lines of prompts to interact with a large language model, we receive sonnets, debugging suggestions, or complex analyses almost instantly.
This software-centric view might obscure a fundamental reality that artificial intelligence is not just a software problem. It is a physics problem involving the movement of electrons through silicon and the challenge of moving massive amounts of data between memory and compute units.
However, sophisticated AI tools like LLMs cannot be built using just CPUs. This is because the CPU was designed for logic, branching decisions, and serial execution. On the other hand, deep learning requires linear algebra, massive parallelism, and probabilistic operations.
In this article, we will look at how GPUs and TPUs help build modern LLMs and the architecture behind them.
AI is a Math Factory
At its core, every neural network performs one fundamental operation billions of times: matrix multiplication.
When we ask an LLM a question, our words are converted into numbers that flow through hundreds of billions of multiply-add operations. A single forward pass through a 70-billion-parameter model requires over 140 trillion floating-point operations.
The mathematical structure is straightforward. Each layer performs Y = W * X + B, where X represents input data, W contains learned parameters, B is a bias vector, and Y is the output. When we scale this to billions of parameters, we are performing trillions of simple multiplications and additions.
What makes this workload special is its reliance on parallel computation. Each multiplication in a matrix operation is completely independent. Computing row 1 multiplied by column 1 does not require waiting for row 2 multiplied by column 2. We can split the work across thousands of processors with zero communication overhead during computation.
The Transformer architecture amplifies this parallelism. The self-attention mechanism calculates relationship scores between every token and every other token. As a reference, for a 4,096-token context window, this creates over 16 million attention pairs. Each transformer layer performs several major matrix multiplications, and a 70-billion-parameter model can execute millions of these operations per forward pass.
Why CPUs Fall Short
The CPU excels at tasks requiring complex logic and branching decisions. Modern CPUs contain sophisticated mechanisms designed for unpredictable code paths, but neural networks do not need these features.
Branch prediction machinery achieves 93-97% accuracy in guessing conditional statement outcomes, consuming significant silicon area. Neural networks, however, have almost no branching. They execute the same operations billions of times with predictable patterns.
Out-of-order execution reorders instructions to keep processors busy while waiting for data. Matrix multiplication has perfectly predictable access patterns that do not benefit from this complexity. Large cache hierarchies (L1, L2, L3) hide memory latency for random access, but neural network data flows sequentially through memory.
This means that only a small percentage of a CPU die is dedicated to arithmetic. Most transistor budget goes to control units managing out-of-order execution, branch prediction, and cache coherency. When running an LLM, these billions of transistors sit idle, consuming power and occupying space that could have been used for arithmetic units.
Beyond the computational inefficiency, CPUs face an even more fundamental limitation: the Memory Wall. This term describes the widening gap between processor speed and memory access speed. Large language models are massive. A 70-billion parameter model stored in 16-bit precision occupies roughly 140 gigabytes of memory. To generate a single token, the processor must read every single one of those parameters from memory to perform the necessary matrix multiplications.
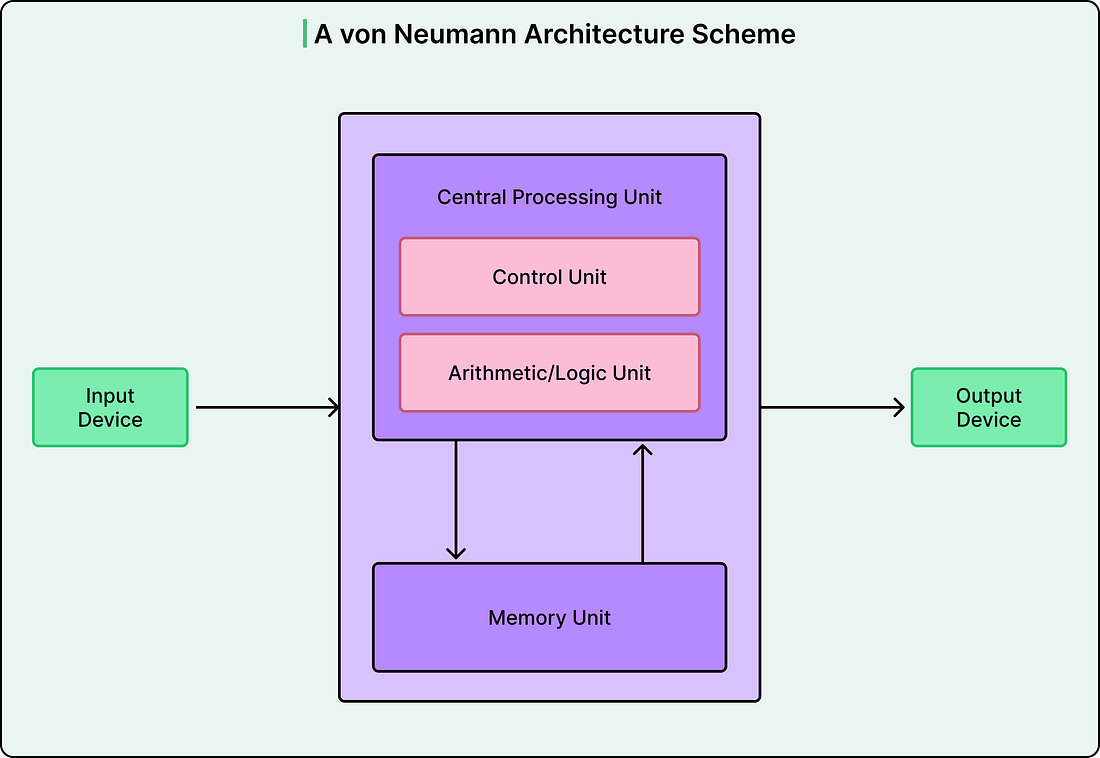
Traditional computers follow the Von Neumann architecture, where a processor and memory communicate through a shared bus. To perform any calculation, the CPU must fetch an instruction, retrieve data from memory, execute the operation, and write results back. This constant transfer of information between the processor and memory creates what computer scientists call the Von Neumann bottleneck.
No amount of increasing core count or clock speed can solve this problem. The bottleneck is not the arithmetic operations but the rate at which data can be delivered to the processor. This is why memory bandwidth, not compute power, often determines LLM performance.
How GPUs Solve the Problem
The Graphics Processing Unit was originally designed to render video games. The mathematical requirements of rendering millions of pixels are remarkably similar to deep learning since both demand massive parallelism and high-throughput floating-point arithmetic.
NVIDIA’s GPU architecture uses SIMT (Single Instruction, Multiple Threads). The fundamental unit is a group of 32 threads called a warp. All threads in a warp share a single instruction decoder, executing the same instruction simultaneously. This shared control unit saves massive silicon area, which is filled with thousands of arithmetic units instead.
While modern CPUs have 16 to 64 complex cores, the NVIDIA H100 contains nearly 17,000 simpler cores. These run at lower clock speeds (1-2 GHz versus 3-6 GHz), but massive parallelism compensates for slower individual operations.
Standard GPU cores execute operations on single numbers, one at a time per thread. Recognizing that AI workloads are dominated by matrix operations, NVIDIA introduced Tensor Cores starting with their Volta architecture. A Tensor Core is a specialized hardware unit that performs an entire matrix multiply-accumulate operation in a single clock cycle. While a standard core completes one floating-point operation per cycle, a Tensor Core executes a 4×4 matrix multiplication involving 64 individual operations (16 multiplies and 16 additions in the multiply step, plus 16 accumulations) instantly. This represents a 64-fold improvement in throughput for matrix operations.
Tensor Cores also support mixed-precision arithmetic, which is crucial for practical AI deployment. They can accept inputs in lower precision formats like FP16 or BF16 (using half the memory of FP32) while accumulating results in higher precision FP32 to preserve numerical accurac